学习平台

AcWing 、 LeetCode

核心套路

数字三角模型【线性DP】

题目1：摘花生

摘花生

思路

动态规划分析

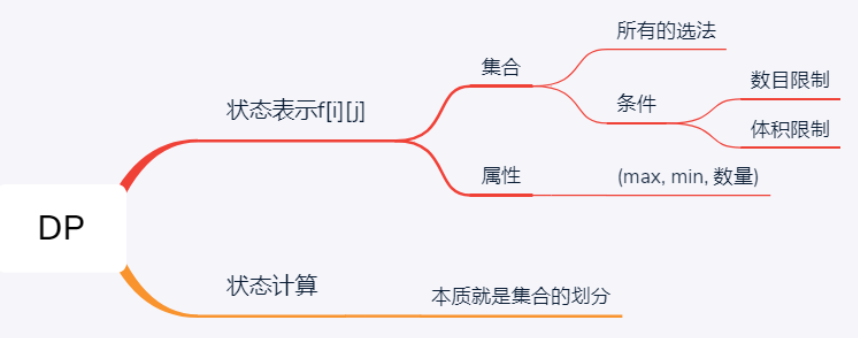
状态表示：f[i][j]
- 集合：走到第 i 行第 j 列时拿到的最大花生数
- 属性：max，（属性的选择有：max，min，数量）
状态计算：状态计算的实质就是 集合划分 ，本题可以根据上一步是从哪个方向来的进行划分
- 选择从北边来的：f[i][j] = f[i - 1][j] + arr[i]
- 选择从西边来的：f[i][j] = f[i][j - 1] + arr[i]

集合划分的原则

一般原则：不重不漏，不重不一定都要满足（一般求数量时要满足）
如何将现有的集合划分为更小的子集，使得所有的子集都可以计算出来。

题解

题解 1

// f[i][j] = max(f[i - 1][j], f[i][j - 1]) + w[i][j]  向南走和向东走的花生数
#include <iostream>
#include <algorithm>

using namespace std;
typedef long long ll;
const int N = 110;
int n, a, b;

int main() {
    scanf("%d", &n);
    while(n --) {
        scanf("%d%d", &a, &b);
        ll f[a + 1][b + 1];
        for(int i = 0; i <= a; i ++)
            for(int j = 0; j <= b; j ++)
                f[i][j] = 0;
        int x;
        for(int i = 1; i <= a; i ++) {
            for(int j = 1; j <= b; j ++) {
                cin >> x;
                f[i][j] = max(f[i - 1][j], f[i][j - 1]) + x;
            }
        }
        cout << f[a][b] << endl;
    }
    return 0;
}

时间复杂度：O(n a b )，其中 n 是数据的组数，a 是每组数据的行数，b 是每组数据的列数
空间复杂度：O(n * n)，需要使用额外的数组保存状态f[][]

执行用时：1122 ms

内存消耗：2520 KB

通过测试用例：10/10

题目2：最低通行费

最低通行费

思路

动态规划分析

因为从左上角走到右下角求最小值并且每个位置的值都是大于0的，所以只能向下或向右走。

因为求最小值，所以第0行和第0列需要赋初始值为1e9

状态表示：f[i][j]
- 集合：走到第 i 行第 j 列时的最低通行费
- 属性：min，（属性的选择有：max，min，数量）
状态计算：状态计算的实质就是 集合划分 ，本题可以根据上一步是从哪个方向来的进行划分
- 选择从北边来的：f[i][j] = f[i - 1][j] + arr[i]
- 选择从西边来的：f[i][j] = f[i][j - 1] + arr[i]

题解

题解 1

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 110;
int n;
int f[N][N];

int main(){
    cin >> n;
    int x;
    for(int i = 0; i <= n; i ++) 
        for(int j = 0; j <= n; j ++)
            f[i][j] = 1e9; // 将所有的f[i][j] = 1e9
    for(int i = 1; i <= n; i ++) {
        for(int j = 1; j <= n; j ++){
            cin >> x;
            if(i == 1 && j == 1) f[i][j] = x; // f[1][1] = x
            else f[i][j] = min(f[i - 1][j], f[i][j - 1]) + x;
        }
    }
    cout << f[n][n] << endl;
    return 0;
}

时间复杂度：O(n n )，其中 n* 是正方形宽度
空间复杂度：O(n * n)，需要使用额外的数组保存状态f[][]

执行用时：33 ms

内存消耗：344 KB

通过测试用例：10/10

题目3：方格取数⭐

方格取数

思路

动态规划分析

状态表示：f[k][i1][i2]
- 集合：表示两条路线分别从[1][1]、[1][1]走到[i1][k - i1]和 [i2][k - i2]的路线的最大值总和。其中 k 保证了两条路线的同步进行。
- 属性：max，（属性的选择有：max，min，数量）
状态计算：状态计算的实质就是 集合划分 ，本题根据从上一步走到当前位置的操作
- 两条路线走到同一位置 i1 == i2：则只需要加一次 w[i1][j1]，否则还需要再加上w[i2][j2]，因此t = w[i1][j1] || t = w[i1][j1] + w[i2][j2]
- i1从上向下，i2从上向下：f[k][i1][i2] = max(f[k][i1][i2], f[k - 1][i1 - 1][i2 - 1] + t)
- i1从上向下，i2从左向右：f[k][i1][i2] = max(f[k][i1][i2], f[k - 1][i1 - 1][i2] + t)
- i1从左向右，i2从上向下：f[k][i1][i2] = max(f[k][i1][i2], f[k - 1][i1][i2 - 1] + t)
- i1从左向右，i2从左向右：f[k][i1][i2] = max(f[k][i1][i2], f[k - 1][i1][i2] + t)

题解

题解 1

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 15;
int n;
int w[N][N];
int f[N * 2][N][N];

int main(){
    cin >> n;
    int a, b, c;
    while(cin >> a >> b >> c, a || b || c) w[a][b] = c;
    
    for(int k = 2; k <= n * 2; k ++) // k 表示横纵坐标之和，从(1, 1)到(n, n)
        for(int i1 = 1; i1 <= n; i1 ++)
            for(int i2 = 1; i2 <= n; i2 ++){
                int j1 = k - i1, j2 = k - i2; // 计算出两条路线对应的纵坐标
                
                if(j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n) { // 纵坐标需要在合法位置
                    int t = w[i1][j1];
                    if(i1 != i2) t += w[i2][j2]; // 若两个位置不重合，需要加上两个位置，否则加一次仅可
                    
                    int &x = f[k][i1][i2]; // 使用 x 代替f[k][i1][i2]
                    x = max(x, f[k - 1][i1 - 1][i2 - 1] + t); // i1下，i2下
                    x = max(x, f[k - 1][i1 - 1][i2] + t); // i1下，i2右
                    x = max(x, f[k - 1][i1][i2 - 1] + t); // i1右，i2下
                    x = max(x, f[k - 1][i1][i2] + t); // i1右，i2右
                }
            }
    cout << f[n + n][n][n] << endl;
    return 0;
}

时间复杂度：O(n n )，其中 n* 是方格的宽度
空间复杂度：O(n n n)，需要使用额外的数组保存状态f[][][]

执行用时：11 ms

内存消耗：216 KB

通过测试用例：11/11

题目3：传纸条⭐

传纸条

思路

和方格取数的解题思想完全一致

动态规划分析

状态表示：f[k][i1][i2]
- 集合：表示两条路线分别从[1][1]、[1][1]走到[i1][k - i1]和 [i2][k - i2]的路线的最大值总和。其中 k 保证了两条路线的同步进行。
- 属性：max，（属性的选择有：max，min，数量）
状态计算：状态计算的实质就是 集合划分 ，本题根据从上一步走到当前位置的操作
- 两条路线走到同一位置 i1 == i2：则只需要加一次 w[i1][j1]，否则还需要再加上w[i2][j2]，因此t = w[i1][j1] || t = w[i1][j1] + w[i2][j2]
- i1从上向下，i2从上向下：f[k][i1][i2] = max(f[k][i1][i2], f[k - 1][i1 - 1][i2 - 1] + t)
- i1从上向下，i2从左向右：f[k][i1][i2] = max(f[k][i1][i2], f[k - 1][i1 - 1][i2] + t)
- i1从左向右，i2从上向下：f[k][i1][i2] = max(f[k][i1][i2], f[k - 1][i1][i2 - 1] + t)
- i1从左向右，i2从左向右：f[k][i1][i2] = max(f[k][i1][i2], f[k - 1][i1][i2] + t)

题解

题解 1

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 55;
int n, m;
int w[N][N];
int f[N * 2][N][N];

int main() {
    cin >> n >> m;
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++)
            cin >> w[i][j];
    
    for(int k = 2; k <= n + m; k ++)
        for(int i1 = 1; i1 <= n; i1 ++)
            for(int i2 = 1; i2 <= n; i2 ++) {
                int j1 = k - i1, j2 = k - i2;
                if(j1 >= 1 && j1 <= m && j2 >= 1 && j2 <= m) {
                    int t = w[i1][j1];
                    if(i1 != i2) t += w[i2][j2];
                    int &x = f[k][i1][i2];
                    x = max(x, f[k - 1][i1 - 1][i2 - 1] + t);
                    x = max(x, f[k - 1][i1 - 1][i2] + t);
                    x = max(x, f[k - 1][i1][i2 - 1] + t);
                    x = max(x, f[k - 1][i1][i2] + t);
                }
            }
    cout << f[n + m][n][n] << endl;
    return 0;
}

时间复杂度：O(n m )，其中 n* 是方格的宽度
空间复杂度：O(n n n)，需要使用额外的数组保存状态f[][][]

执行用时：33 ms

内存消耗：1112 KB

通过测试用例：10/10

最长上升子序列模型

题目1：怪盗基德的滑翔伞

怪盗基德的滑翔伞

思路

动态规划分析

状态表示：f[i]
- 集合：表示以第 i 个数据结尾的数值上升子序列的集合
- 属性：max，（属性的选择有：max，min，数量）
状态计算：状态计算的实质就是 集合划分 ，本题根据上升子序列的倒数第二位是数组中的第几个数
- 第 i 个数据就是最长上升子序列的第一位，则f[i] = 1
- 第 j 个数据是以第 i 个数据结尾的最长上升子序列的倒数第二个位，则需要满足 1 <= j <= i && a[j] < a[i],则f[i] = f[j] + 1

题解

题解 1

// f[i] 表示以第i个数结尾的数值上升子序列的集合  max
// f[i] 按照前一位是第几个数字划分，j从 1到i，
// f[i] 初始为1，前面没有比第i个数字小的
// 若a[j] < a[i] 则 f[i] = max(f[i], f[j] + 1);

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 110;
int k, n;
int a[N], f[N], d[N];

int main() {
    cin >> k;
    while(k --) {
        cin >> n;
        int resUp = 0, resDown = 0;
        for(int i = 1; i <= n; i ++)
            cin >> a[i];
        
        for(int i = 1; i <= n; i ++){  // 求上升子序列
            f[i] = 1;
            for(int j = 1; j <= i; j ++) {
                if(a[i] > a[j])
                    f[i] = max(f[i], f[j] + 1);
            }
        }
        for(int i = 1; i <= n; i ++) {  // 求下降子序列
            d[i] = 1;
            for(int j = 1; j <= i; j ++) {
                if(a[i] < a[j])
                    d[i] = max(d[i], d[j] + 1);
            }
        }
        for(int i = 1; i <= n; i ++){
            resUp = max(resUp, f[i]);
            resDown = max(resDown, d[i]);
        }
        cout << max(resDown, resUp) << endl;
    }
    return 0;
}

时间复杂度：O(n n)，其中 n* 是建筑的个数
空间复杂度：O(n)，需要使用额外的数组保存状态f[]

执行用时：88 ms

内存消耗：344 KB

通过测试用例：10/10 个数据

题目2：登山⭐

登山

思路

根据题意分析可知，本题是先上升子序列到某个点之后是下降子序列，因此需要分别求出上升子序列和下降子序列，然后遍历一遍，找出在某个点上升子序列加上下降子序列并减一最大，因为在最高点的时候加了两次。

动态规划分析

状态表示：f[i]、d[i]
- 集合：f[i]表示以第 i 个数据结尾的数值上升子序列的集合，f[i]表示以第 i 个数据开始的数值下降子序列的集合（就是从后往前找上升子序列）
- 属性：max，（属性的选择有：max，min，数量）
状态计算：状态计算的实质就是 集合划分 ，本题根据上升子序列的倒数第二位是数组中的第几个数
- 第 i 个数据就是最长上升子序列的第一位，则f[i] = 1
- 第 j 个数据是以第 i 个数据结尾的最长上升子序列的倒数第二个位，则需要满足 1 <= j <= i && a[j] < a[i],则f[i] = f[j] + 1

题解

题解 1

// 最开始可能是上升子序列，当走到某个点后，不能继续上升了，转为下降子序列。

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 1010;

int n;
int a[N], f[N], d[N];

int main() {
    cin >> n;
    int res = 0;
    for(int i = 1; i <= n; i ++) cin >> a[i];
    
    for(int i = 1; i <= n; i ++){  // 从前往后求上升子序列
        f[i] = 1;
        for(int j = 1; j < i; j ++) 
            if(a[i] > a[j])
                f[i] = max(f[i], f[j] + 1);
    }
    
    for(int i = n; i; i --) {  // 从后往前求上升子序列
        d[i] = 1;
        for(int j = n; j > i; j --)
            if(a[i] > a[j])
                d[i] = max(d[i], d[j] + 1);
    }
    
    for(int i = 1; i <= n; i ++) res = max(res, f[i] + d[i] - 1); // 在顶点位置多加了1
    cout << res << endl;
    return 0;
}

时间复杂度：O(n n)，其中 n* 是景点个数
空间复杂度：O(n)，需要使用额外的数组保存状态f[]

执行用时：51 ms

内存消耗：216 KB

通过测试用例：11/11 个数据

题目3：合唱队形

合唱队形

思路

和【题目2：登山】思路完全一样

题解

题解 1

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 110;
int n;
int a[N], f[N], g[N];

int main() {
    cin >> n;
    for(int i = 1; i <= n; i ++) cin >> a[i];
    for(int i = 1; i <= n; i ++){
        f[i] = 1;
        for(int j = 1; j < i; j ++)
            if(a[i] > a[j])
                f[i] = max(f[i], f[j] + 1);
    }
    
    for(int i = n; i ; i--){
        g[i] = 1;
        for(int j = n; j > i; j --)
            if(a[i] > a[j])
                g[i] = max(g[i], g[j] + 1);
    }
    
    int res = 0;
    for(int i = 1; i <= n; i ++) res = max(res, f[i] + g[i] - 1);
    cout << n - res << endl;
    return 0;
}

时间复杂度：O(n n)，其中 n* 是学生个数
空间复杂度：O(n)，需要使用额外的数组保存状态f[]

执行用时：20 ms

内存消耗：220 KB

通过测试用例：11/11 个数据

题目4：友好城市⭐

友好城市

思路

分析：建造的桥互不影响，按照左边城市编号从小到大进行排序后，与自己对应的右边城市也应该时从小到大的。否则就会交叉。

所以可以使用pair<int, int>进行保存每对友好城市的编号，然后以first进行排序后，对排序后的second编号求最长上升子序列即可。

题解

题解 1

#include <iostream>
#include <algorithm>

using namespace std;
typedef pair<int, int> PII;
const int N = 5010;

int n;
PII q[N];
int f[N];

int main() {
    cin >> n;
    for(int i = 0; i < n; i ++) scanf("%d%d", &q[i].first, &q[i].second);
    
    sort(q, q + n); // 按照左边的数进行从小到大排序
    int res;
    for(int i = 0; i < n; i ++){
        f[i] = 1;
        for(int j = 0; j < i; j ++) {
            if(q[i].second > q[j].second)
                f[i] = max(f[i], f[j] + 1);
        }
        
        res = max(res, f[i]);
    }
    
    cout << res << endl;
    return 0;
}

时间复杂度：O(n n)，其中 n* 是城市个数
空间复杂度：O(n)，需要使用额外的数组保存状态f[]

执行用时：284 ms

内存消耗：352 KB

通过测试用例：10/10 个数据

题目4：最大上升子序列的和

最大上升子序列的和

思路

动态规划分析

状态表示：f[i]
- 集合：表示以第 i 个数据结尾的数值上升子序列的和
- 属性：max，（属性的选择有：max，min，数量）
状态计算：状态计算的实质就是 集合划分 ，本题根据上升子序列的倒数第二位是数组中的第几个数
- 第 i 个数据就是最长上升子序列的第一位，则f[i] = 1
- 第 j 个数据是以第 i 个数据结尾的最长上升子序列的倒数第二个位，则需要满足 1 <= j <= i && a[j] < a[i],则f[i] = f[j] + a[i]

题解

题解 1

// 表示以i结尾的最大上升子序列的和
#include <iostream>
#include <algorithm>

using namespace std;
const int N = 1010;
int n;
int a[N], f[N];

int main() {
    cin >> n;
    for(int i = 1; i <= n; i ++) cin >> a[i];
    
    for(int i = 1; i <= n; i ++) {
        f[i] = a[i];
        for(int j = 1; j < i; j ++){
            if(a[i] > a[j])
                f[i] = max(f[i], f[j] + a[i]);
        }
    }
    int res = 0;
    for(int i = 1; i <= n; i++) res = max(res, f[i]);
    cout << res << endl;
    return 0;
}

时间复杂度：O(n n)，其中 n* 是序列长度
空间复杂度：O(n)，需要使用额外的数组保存状态f[]

执行用时：39 ms

内存消耗：216 KB

通过测试用例：11/11 个数据

题目5：拦截导弹❗

思路

本题难点：处理数据的输入、第二小问

第一小问的解题思路就是【最长上升子序列】的标准解题思路。

第二小问不理解

题解

题解 1

#include <sstream>
#include <iostream>
#include <algorithm>

using namespace std;
const int N = 1010;

int n;
int h[N], f[N], q[N];

int main() {
    // 处理一整行输入
    string line;
    getline(cin, line);
    stringstream ssin(line);
    while(ssin >> h[n]) n ++;
    
    // dp
    int res = 0, cnt = 0;
    for(int i = 0; i < n; i ++) {
        f[i] = 1;
        for(int j = 0; j < i; j ++) {
            if(h[j] >= h[i])
                f[i] = max(f[i], f[j] + 1);
        }
        res = max(res, f[i]);  // 计算最多能拦截的导弹数
        
        // 不太理解
        int k = 0;
        while (k < cnt && q[k] < h[i]) k ++ ;
        if (k == cnt) q[cnt ++ ] = h[i];
        else q[k] = h[i];
    }
    
    
    cout << res << endl;
    cout << cnt << endl;
    return 0;
}

时间复杂度：O(n n)，其中 n* 是序列长度
空间复杂度：O(n)，需要使用额外的数组保存状态f[]

执行用时：39 ms

内存消耗：216 KB

通过测试用例：11/11 个数据

背包模型

题目1：背包问题

背包问题

思路

动态规划分析

状态表示：f[i][j]
- 集合：只从前 i 个物品中选择并且总体积小于等于 j 的所有选法。
- 属性：max，（属性的选择有：max，min，数量）
状态计算：状态计算的实质就是 集合划分 ，本题可以根据是否选择第 i 件物品来划分
- 不选择第 i 件物品：f[i][j] = f[i - 1][j]
- 选择第 i 件物品：可以先计算不选择第 i 件物品并且总体积不超过 j - v[i]的选法再加上第 i 件物品的价值w[i]。所以最后的表示为： f[i][j] = f[i - 1][j - v[i]] + w[i]

集合划分的原则 ⭐

一般原则：不重不漏，不重不一定都要满足（一般求数量时要满足）
如何将现有的集合划分为更小的子集，使得所有的子集都可以计算出来。

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;
const int N=1010;

int n, m;
int f[N][N];
int v[N], w[N];

int main(){
    cin >> n >> m;//n个物品，背包容量是m
    for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; i++)
        for(int j = 0; j <= m; j++){
            f[i][j] = f[i - 1][j];
            if(j >= v[i]){  // 当第i件物品的体积不超过j时
                f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
            }
        }
    int res = 0;
    for(int i = 0; i <= m; i++)
        res = max(res, f[n][i]);
    cout << res;
    return 0;
}

时间复杂度：O(n m)，其中 n 和 m* 分别是物品数和背包体积
空间复杂度：O(n * m)

执行用时：54 ms

内存消耗：4184 KB

通过测试用例：10/10

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];

int main() {
    cin >> n >> m;
    for(int i = 1; i <= n; i ++)
        cin >> v[i] >> w[i];
    for(int i = 1; i <= n; i ++)
        for(int j = m; v[i] <= j; j --)  // 从大到小判断是为了求解f[j - v[i]] + w[i]时的仍然时i - 1层的
            f[j] = max(f[j], f[j - v[i]] + w[i]);
    cout << f[m] << endl;
    return 0;
}

时间复杂度：O(n m)，其中 n 和 m* 分别是物品数和背包体积
空间复杂度：O(n * m)

执行用时：54 ms

内存消耗：4184 KB

通过测试用例：10/10

题目2：完全背包问题

完全背包问题

思路

动态规划分析

状态表示：f[i][j]
- 集合：只从前 i 个物品中选择并且总体积小于等于 j 的所有选法。
- 属性：max，（属性的选择有：max，min，数量）
状态计算：状态计算的实质就是 集合划分 ，本题可以根据选择 k 个第 i 件物品来划分
- 选择第 k 个第 i 件物品：和 背包问题 中的选择第 i 件物品类似，f[i][j] = f[i - 1][j - k * v[i]] + k * w[i]，其中 k ∈ {0, 1, 2, ..., s[i]}

题解

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];

int main() {
    cin >> n >> m;
    for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
   	
    for(int i = 1; i <= n; i ++)
        for(int j = 0; j <= m; j ++)
            for(int k = 0; k * v[i] <= j; k ++){  // 遍历第i个物品的选择个数
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
            }
    cout << f[n][m] << endl;
    return 0;
}

时间复杂度：O(n m)，其中 n 和 m* 分别是物品数和背包体积
空间复杂度：O(n * m)

执行用时：54 ms

内存消耗：4184 KB

通过测试用例：10/10

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];

int main() {
    cin >> n >> m;
    for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
    for(int i = 1; i <= n; i ++)
        for(int j = 0; j <= m; j ++){
            f[i][j] = f[i - 1][j];
            if(j >= v[i])
                f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
        }
    cout << f[n][m] << endl;
    return 0;
}

时间复杂度：O(n m)，其中 n 和 m* 分别是物品数和背包体积
空间复杂度：O(n * m)

执行用时：54 ms

内存消耗：4184 KB

通过测试用例：10/10

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 1010;

int n, m;
int v[N], w[N];
int f[N];

int main() {
    cin >> n >> m;
    for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; i ++)
        for(int j = v[i]; j <= m; j ++)
            f[j] = max(f[j], f[j - v[i]] + w[i]);
    
    cout << f[m] << endl;
    return 0;
}

时间复杂度：O(n m)，其中 n 和 m* 分别是物品数和背包体积
空间复杂度：O(n * m)

执行用时：54 ms

内存消耗：4184 KB

通过测试用例：10/10

题目3：采药

采药

思路

动态规划分析

状态表示：f[i][j]
- 集合：只从前 i 个物品中选择并且总体积小于等于 j 的所有选法。
- 属性：max，（属性的选择有：max，min，数量）
状态计算：状态计算的实质就是 集合划分 ，本题可以根据是否选择第 i 件物品来划分
- 不选择第 i 件物品：f[i][j] = f[i - 1][j]
- 选择第 i 件物品：可以先计算不选择第 i 件物品并且总体积不超过 j - v[i]的选法再加上第 i 件物品的价值w[i]。所以最后的表示为： f[i][j] = f[i - 1][j - v[i]] + w[i]

题解

二维表示
一维表示-优化

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;
const int N=1010;

int n, m;
int f[N][N];
int v[N], w[N];

int main(){
    cin >> n >> m;//n个物品，背包容量是m
    for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; i++)
        for(int j = 0; j <= m; j++){
            f[i][j] = f[i - 1][j];
            if(j >= v[i]){  // 当第i件物品的体积不超过j时
                f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
            }
        }
    int res = 0;
    for(int i = 0; i <= m; i++)
        res = max(res, f[n][i]);
    cout << res;
    return 0;
}

时间复杂度：O(n m)，其中 n 和 m* 分别是物品数和背包体积
空间复杂度：O(n * m)

执行用时：18 ms

内存消耗：604 KB

通过测试用例：10/10 个数据

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 110, M = 1010;

int n, m;
int w[N], v[N];
int f[M];  // f[i][j] 表示拿到第i个物品并且总重量不超过j的价值

int main() {
    cin >> m >> n;  // n：总体积， m：物品个数
    
    for(int i = 1; i <= n; i ++)
        cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; i ++)
        for(int j = m; j >= v[i]; j --) { // 总体积
            f[j] = max(f[j], f[j - v[i]] + w[i]);  // 拿第i个物品
        }
    
    cout << f[m] << endl;
    return 0;
}

时间复杂度：O(n m)，其中 n 和 m* 分别是物品数和背包体积
空间复杂度：O(n)

执行用时：18 ms

内存消耗：220 KB

通过测试用例：10/10 个数据

题目4：装箱问题

装箱问题

思路

基础【01背包】问题

题解

一维表示-优化

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 40, V = 20010;
int n, m; // n 物品个数
int v[N];
int f[V]; // f[j]表示总体积不超过j的物品总体积，最大值

int main(){
    cin >> m >> n;
    for(int i = 1; i <= n; i ++) cin >> v[i];
    // for(int i = 0; i <= m; i ++) f[i] = n;
    
    for(int i = 1; i <= n; i ++)
        for(int j = m; j >= v[i]; j --){
            f[j] = max(f[j], f[j - v[i]] + v[i]);
        }
    cout << m - f[m] << endl;
    return 0;
}

时间复杂度：O(n m)，其中 n 和 m* 分别是物品数和背包体积
空间复杂度：O(n)

执行用时：19 ms

内存消耗：344 KB

通过测试用例：8/8 个数据

题目5：宠物小精灵之收服⭐⭐

宠物小精灵之收服

思路

【二维01背包问题】

动态规划分析

状态表示：f[i][j][k]
- 集合：只从前 i 个物品中选择并且花费1小于等于 j 并且花费2不超过 k 的所有选法。下面的题解按照01背包问题的优化方法进行了优化，所以只需要二维。
- 属性：max，（属性的选择有：max，min，数量）
状态计算：状态计算的实质就是 集合划分 ，本题可以根据是否选择第 i 件物品来划分
- 不选择第 i 件物品：f[i][j][k] = f[i - 1][j][k]
- 选择第 i 件物品：可以先计算不选择第 i 件物品并且总体积不超过 j - v[i]的选法再加上第 i 件物品的价值w[i]。所以最后的表示为： f[i][j][k] = f[i - 1][j - v1[i]][k - v2[i]] + w[i]

另外本题存在陷阱，当精零体力值小于等于0时不能被抓，所以最后输出的结果是 f[m][t - 1]，至少保留一滴体力。

题解

二维表示-优化

#include <iostream>

using namespace std;
const int N = 110, M = 1010, K = 510;
int m, t, n; // m精灵球数量，t初始体力值，n小精灵数量
int v1[N], v2[N]; // v1需要的精灵球数，v2对皮卡丘造成的伤害
int f[M][K]; 
// f[i][j][k] 表示只从前i个数中选择并且花费1不超过j并且花费2不超过k的所有选法的最大值。
// 优化一维，变成两维。

int main() {
    cin >> m >> t >> n;
    
    for(int i = 1; i <= n; i ++) cin >> v1[i] >> v2[i];
    
    //dp
    for(int i = 1; i <= n; i ++) 
        for(int j = m; j >= v1[i]; j --)
            for(int k = t - 1; k >= v2[i]; k --) {
                f[j][k] = max(f[j][k], f[j - v1[i]][k - v2[i]] + 1);
            }
    cout << f[m][t - 1] << " ";  // 因为精灵体力小于等于0也不会被收服，所以需要t - 1
    
    //找到满足 最大价值 的所有状态里，第二维费用消耗最少的
    int const_health = t;
    for(int k = 0; k <= t - 1; k ++) {
        if(f[m][k] == f[m][t - 1]) { 
            const_health = min(const_health, k);
        }
    }
    cout << t - const_health << endl;
    return 0;
}

时间复杂度：O(n m t)，其中 m精灵球数量，t初始体力值，n小精灵数量
空间复杂度：O(m * k)

执行用时：841 ms

内存消耗：2268 KB

通过测试用例：13/13 个数据

题目6：数字组合⭐

数字组合

思路

本题和上面【01背包问题】不同的点是属性，本题求解的属性是数量count

动态规划分析

状态表示：f[i][j]
- 集合：只从前 i 个物品中选择并且总体积小于等于 j 的所有选法。
- 属性：count，（属性的选择有：max，min，count）
状态计算：状态计算的实质就是 集合划分 ，本题可以根据是否选择第 i 件物品来划分
- 不选择第 i 件物品：f[i][j] = f[i - 1][j]
- 选择第 i 件物品：可以先计算不选择第 i 件物品并且总体积不超过 j - v[i]的选法。所以最后的表示为： f[i][j] = f[i - 1][j - v[i]]
- 所以f[i][j] = f[i - 1][j] + f[i - 1][j - v[i]]

题解

二维

// 只从前i个物品中选并且恰好是j的 数量
// 属性：数量
#include <iostream>
#include <algorithm>

using namespace std;
const int N = 110, M = 10010;
int n, m;
int a[N];
int f[M];

int main() {
    cin >> n >> m;
    for(int i = 1; i <= n; i ++) cin >> a[i];
    
    f[0] = 1; // f[0][0] = 1; 空集
    for(int i = 1; i <= n; i ++)
        for(int j = m; j >= a[i]; j --){
            f[j] = f[j] + f[j - a[i]];  // 不选第i个 + 选第i个
        }
    
    cout << f[m];
    return 0;
}

时间复杂度：O(n * m)，其中 n 是整数个数，m 是目标和
空间复杂度：O(m)

执行用时：15 ms

内存消耗：344 KB

通过测试用例：11/11 个数据

题目7：买书

思路

和【数字组合】思路类似，需要明确背包的体积：小明拥有的钱数，每个物品的体积：每本书的价格。

题解

二维

#include <iostream>

using namespace std;
const int N = 1010;
int n;
int a[5] = {0, 10, 20, 50, 100};
int f[N];

int main() {
    cin >> n;
    f[0] = 1;
    for(int i = 1; i <= 4; i ++) {
        for(int j = a[i]; j <= n; j ++)
            f[j] = f[j] + f[j - a[i]];
    }
    cout << f[n];
    return 0;
}

时间复杂度：O(n)，其中 n 是小明拥有的钱数
空间复杂度：O(m)

执行用时：15 ms

内存消耗：216 KB

通过测试用例：10/10 个数据

题目8：货币系统

思路

和【数字组合】思路类似，需要明确背包的体积：需要组成的面值m，每个物品的体积：每个货币的面值，物种数量：n

题解

二维

#include <iostream>
#include <algorithm>

using namespace std;
typedef long long ll;
const int N = 20, M = 3010;

int n, m;
int a[N];
ll f[M];  // f[j] 表示面值为j的方案数。

int main() {
    cin >> n >> m;
    for(int i = 1; i <= n; i ++) cin >> a[i];
    
    f[0] = 1;
    for(int i = 1; i <= n; i ++)
        for(int j = a[i]; j <= m; j ++)
            f[j] += f[j - a[i]];
    cout << f[m] << endl;
    return 0;
}

时间复杂度：O(n * m)，其中 n 是货币种类数，m是面值
空间复杂度：O(m)

执行用时：12 ms

内存消耗：220 KB

通过测试用例：11/11 个数据

状态机模型

状态压缩DP

状态压缩DP

棋盘式（基于连通性）
集合

区间DP

题目1：石子合并

石子合并

思路

动态规划分析

状态表示：f[i][j]
- 集合：所有将第 i 堆石子到第 j 堆石子合并成一堆石子的合并方式
- 属性：min
状态计算：本质就是 集合划分 ，以分界线的位置进行分类。
- 将区间分为f[i][k] 和 f[k + 1][j]，则总代价为f[i][k] + f[k + 1][j] +s[j] - s[i - 1]， s[]为前缀和数组
- f[i][j] = main(f[i][k] + f[k + 1][j] +s[j] - s[i - 1])，k ∈ { i ~ j -1 }

题解

区间DP

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 1010;
int n;
int s[N];
int f[N][N];

int main() {
    cin >> n;
    for(int i = 1; i <= n; i ++) cin >> s[i];
    
    for(int i = 1; i <= n; i ++) s[i] += s[i - 1];
    
    for(int len = 2; len <= n; len ++) // 遍历需要计算的石子的个数
        for(int i = 1; i + len - 1 <= n; i ++){ // 遍历当前堆中的左右边界
            int l = i, r = i + len - 1;
            f[l][r] = 1e9; // 初始话f[][]数组
            for(int k = l; k < r; k ++) { // 在左右边界内再将石子划分为两堆
                f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]); 
            }
        }
    cout << f[1][n] << endl;
    return 0;
}

时间复杂度：O(n ^ 3)，其中 n 是石子的个数
空间复杂度：O(n * n)，需要使用额外的数组保存状态f[][]

执行用时：157 ms

内存消耗：1368 KB

通过测试用例：11/11