Atopos's Blog

One step at a time!

0%

AcWing 算法基础课

发表于 更新于 分类于 ，
本文字数： 16k 阅读时长 ≈ 14 分钟
根据AcWing平台上算法基础课的学习编写，本模块的所有模板均来自于AcWing算法基础课，算法思想描述仅供自己理解。

学习平台

AcWing 算法基础课

基础算法

快速排序

算法思想 分治

分支算法可分为三步：

  • 分成子问题
  • 递归处理子问题
  • 子问题合并

代码模板

1
2
3
4
5
6
7
8
9
10
11
12
13
// 快速排序：先排序后分治
void Quick_sort(int p[],int l,int r){
    if(l >= r) return;  // 边界问题

    int x = p[l + r >> 1], i = l - 1, j = r + 1;  // 分界点(哨兵)取中间值
    while(i < j){
        do i++ ;while(p[i] < x);  // 在左边找到第一个比哨兵大的数
        do j-- ;while(p[j] > x);  // 在右边找到第一个比哨兵小的数
        if(i < j) swap(p[i],p[j]);  // 交换左右两边的两个数
    }
    Quick_sort(p, l, j);  // 递归排序左边界
    Quick_sort(p, j + 1, r);  // 递归排序有边界
}

归并排序

算法思想 分治

代码模板 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 归并排序：线分治后排序
void Merge_sort(int p[],int l,int r){
    if(l >= r)return ;

    //这里的中间值不能取(l+r+1)/2
    int mid = l + r >> 1;
    Merge_sort(p,l,mid);
    Merge_sort(p,mid+1,r);

    //合并两个有序数组，
    int k=0,i = l,j = mid + 1;
    while(i <= mid && j <= r)
        if(p[i] <= p[j]) tmp[k ++] = p[i ++];
        else tmp[k ++] = p[j ++];

    while(i <= mid) tmp[k ++]=p[i ++];
    while(j <= r) tmp[k ++]=p[j ++];

    for(i = l, j = 0;i <= r; i ++, j ++) p[i]=tmp[j];
    //i=l是因为l永远是分组的左边界，不能写成i=0,同理r也永远是分组的右边界
}

二分查找

算法思想 二分

实现思想 假定目标值在区间[l, r] 中，每次将区间长度缩小一半，当l = r 时，则可以取到目标值。

整数二分查找存在两个模板，取决于中间值的取值方法：

  • 当mid = l + r >> 1 时：

代码模板 

1
2
3
4
5
6
7
8
int bsearch(int l, int r){
    while(l < r){
        int mid = l + r >> 1;
        if(check(mid)) r = mid;
        else l = mid + 1;
    }
    return l;
}
  • 当mid = l + r + 1 >> 1 时：

代码模板 

1
2
3
4
5
6
7
8
int bsearch(int l, int r){
    while(l < r){
        int mid = l + r + 1 >> 1;
        if(check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

高精度加法

算法思想 大数加法 ；

代码模板 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
vector<int> add(vector<int> &A, vector<int> &B){
    if(B.size() > A.size()) return add(B,A);  // 让两个大数中长度相对较短的做B，相对较长的做A

    vector<int> C;  // 用于存放结果
    int t = 0; // 存放进位
    for(int i = 0;i < A.size(); i ++){
        t += A[i];
        if(i < B.size()) t += B[i]; //如果B还没有遍历完，需要加上对应位置，若遍历完，则不需要加上了。
        C.push_back(t % 10); // 若有进位，则只存放个位数字
        t /= 10; //将进位保存
    }
    if(t) C.push_back(t); //最后有进位的话（进位一定是个位数），将进位加入C
    
    return C;
}

高精度减法

算法思想 大数减法 ；

代码模板 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
// A - B;需要首先使用bmp函数判断A是否大于B；若A大于B，则结果为正数并sub(A, B)；若A小于B，则结果为负数，需要先输出'-'并sub(B, A)

//判断A是否大于B，若是则返回true,否则返回false
bool bmp(vector<int> &A, vector<int> &B){
    if(A.size() != B.size()) return A.size() > B.size();
    for(int i = A.size() - 1; i >= 0; i --)  // 长度相同时，从后往前遍历比较大小
        if(A[i] != B[i])
            return A[i] > B[i];
    return true; //相等
}

//高精度减法
vector<int> sub(vector<int> &A, vector<int> &B){
    vector<int> C;
    int t= 0;
    for(int i=0;i < A.size();i++){
        t = A[i] - t; // 若之前有借位，则需要先减去借位
        if(i < B.size()) t -= B[i];
        C.push_back((t + 10) % 10);
        if(t < 0) t = 1;// t < 0 证明有借位
        else t=0;
    }

    //这个判断是为了确保结果不是0，若结果是0，则最后一个0不需要去掉
    while (C.size() > 1 && C.back() == 0) C.pop_back(); //取出前导0  若结果为003，则需要去掉00
    return C;
}

高精度乘低精度

算法思想 大数乘法

代码模板 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// C = A * b, A >= 0, b >= 0
vector<int> mul(vector<int> &A, int b)
{
    vector<int> C;

    int t = 0;
    for (int i = 0; i < A.size() || t; i ++ )
    {
        if (i < A.size()) t += A[i] * b;
        C.push_back(t % 10);
        t /= 10;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();

    return C;
}

高精度除以低精度

算法思想 大数除法

代码模板 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// A / b = C ... r, A >= 0, b > 0
vector<int> div(vector<int> &A, int b, int &r)
{
    vector<int> C;
    r = 0;
    for (int i = A.size() - 1; i >= 0; i -- )
    {
        r = r * 10 + A[i];
        C.push_back(r / b);
        r %= b;
    }
    reverse(C.begin(), C.end());
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

前缀和

什么是前缀和

原数组：a[1], a[2], a[3], a[4], a[5], …, a[n]
前缀和：S[i]为数组的前 i项和
前缀和：S[i] = a[1] + a[2] + a[3] + … + a[i]

为方便求解，以及后续方便计算，通常令S[0] = 0 ,原数组 以及前缀和数组 的下标从1开始。

前缀和的作用

快速求出元素组中某段区间的和。

代码模板 

1
2
3
4
5
6
7
int pSum(int arr[]){
    int sum[N];  // 存放数组的前缀和
    sum[0] = 0;
    for(int i = 1; i <= n; i++){
        sum[i] = arr[i] + sum[i - 1];
    }
}

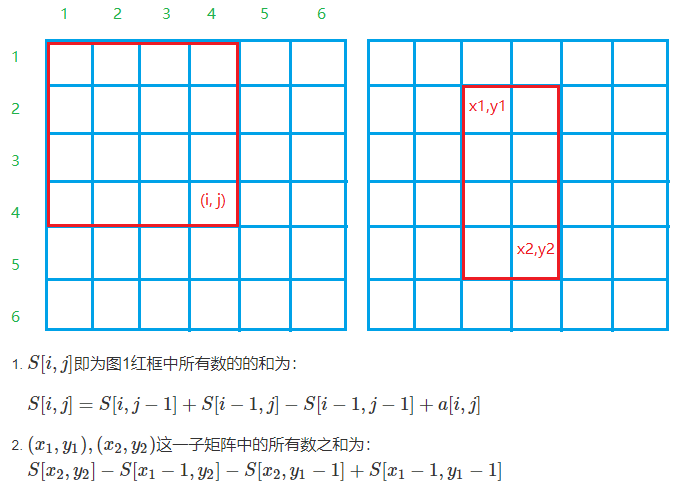
二维数组求解前缀和

计算过程 s[i, j] = s[i - 1, j] + s[i, j - 1] + s[i - 1, j - 1] + a[i, j]

前缀和

同样的为了方便计算，二维数组下标也需要从 1 开始

代码模板 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <iostream>

using namespace std;

const int N = 1010;

int a[N][N], s[N][N];

int main() {
    int n, m, q;
    cin >> n >> m >> q;

    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++) {
            scanf("%d", &a[i][j]);
            s[i][j] = s[i][j - 1] + s[i - 1][j] - s[i - 1][j - 1] + a[i][j]; // 求前缀和
        }

    while (q--) {
        int x1,y1,x2,y2;
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        // 算子矩阵的和
        printf("%d\n", s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1]); 
    }

    return 0;
}

差分

差分 和 前缀和 是一对互逆运算

定义 对于一个给定的数列A，他的差分序列B定义为：

B[1] = A[1], B[i] = A[i] - A[i - 1](2 <= i <= n)

数据结构

单链表

这里采用数组模拟链表，因为采用new Node()的过程是比较慢的；

  • 单链表：可以用于实现邻接表(存储树或图)
  • 双链表：优化某些问题

实现方法 单链表使用数组模拟的方法：使用两个数组e[n]; ne[n] 其中e[i]存放第i个元素的值，ne[i]存放第i个元素的后继下标。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include<iostream>

using namespace std;
const int N = 100010;

//head 表示头节点的下标
//e[i] 表示节点i的值
//ne[n] 表示节点i的next的值
//idx 存储当前已经用到了哪个点
int head, e[N], ne[N], idx;

// 初始化链表
void init(){
    head = -1;
    idx = 0;
}

// 将x插到头节点之前
void add_to_head(int x){
    e[idx] = x;
    ne[idx] = head;
    head = idx;
    idx ++；
}

//删除 下标是k的 后面的节点
void del(int k){
    ne[k] = ne[ne[k]];  // 相当于 p->next = p->next->next
}

//在下标为k的节点后插入一个数
void add(int k, int x){
    e[idx] = x;
    ne[idx] = ne[k];
    ne[k] = idx ++;
}

int main(){
  	init(); 
    return 0;
}

双链表

同样使用数组模拟双链表，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include<iostream>

using namespace std;
const int N = 100010;

int e[N], l[N], r[N], idx;

// 在下标是k的节点右边插入x
void add(int k, int x){  //在k的左边插入的话，直接调用 add(l[k], x)
    e[idx] = x;
    r[idx] = r[k];
    l[idx] = k;
    r[k] = idx;
    l[r[idx]] = idx ++;
}
//删除下标为k的节点
void remove(int k){
    r[l[k]] = r[k];
    l[r[k]] = l[k];
}

栈

采用数组模拟栈

实现方法 top栈顶指针，当top == 0时栈空，stk[N]存放元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include<iostream>
#include<string>

using namespace std;
const int N = 100010;

int top, stk[N];

int main(){
    int m;
    cin >> m;
    while(m --){
        string op;
        int x;
        cin >> op;
        if(op == "push"){  //入栈
            cin >> x;
            stk[++ top] = x;
        }
        else if(op == "pop") top --;  // 出栈
        else if(op == "query") cout << stk[top] <<endl;  //输出栈顶元素
        else cout << (top ? "NO" : "YES") << endl; // 判断栈是否为空，top为0 则栈空
    }
    return 0;
}

队列

采用数组模拟队列

实现方法 tail队尾指针，head队头指针，当head == 0 || head > tail时队空，que[N]存放元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<iostream>
#include<string>

using namespace std;
const int N = 100010;

int head, que[N], tail;

int main(){
    int m;
    cin >> m;
    while(m--){
        string op;
        cin >> op;
        int x;
        if(op == "push"){
            cin >> x;
            que[++tail] = x;
            if(head == 0) head++;
        }
        else if(op == "pop") head ++;
        else if(op == "query") cout << que[head] << endl;
        else{
            if(head == 0 || tail < head) cout << "YES" << endl;
            else cout << "NO" << endl;
        }
    }
}

KMP

定义 是一个字符串匹配算法，对暴力的那种一一比对的方法进行了优化，使时间复杂度大大降低，

算法习惯 下标从1开始；存在一个模式串、一个模板串

算法精讲

KMP字符串

算法思路

  • s[n]模式串：即比较长的字符串
  • p[m]模板串：即比较短的字符串
  • ne[m]部分匹配值表：存储的是每一个下标对应的部分匹配值

p[1, j] == p[i - ne[j] + 1, i]

KMP

  • 核心思想：在每次匹配失败后，不是把p串向后移动一位，而是把p串往后移动至下一次可以和前面部分匹配的位置，这样就可以跳过大多数的失配步骤。而每次p串移动的步数就是通过查找ne[ ]数组确定的。

匹配思路和实现代码

KMP主要分为两步：求解ne数组 ；匹配字符串

s[n]和p[m]都是从1开始的，

  • 求解ne数组

因为p[m]下标从1开始，所以ne[1] = 0，求解ne[]时直接从下标为2开始遍历，i 。j表示当前前面最多匹配了j个字符。

1
2
3
4
5
6
7
8
9
// 手动模拟一遍更清楚。
for(int i = 2, j = 0; i <= m; i++) // ne[1]默认为0
{
    while(j && p[i] != p[j + 1]) j = next[j]; //若已经匹配了字符，但是当前又不匹配了，则j需要返回起点。

    if(p[i] == p[j + 1]) j++;

    next[i] = j;
}
  • 匹配字符串

i 从1开始遍历s数组，j 从0开始遍历p数组。每次将s[i]和p[j + 1]进行比较。若相等，则匹配；若碰到第i个字符不匹配，则直接将j = ne[j]，i 不变。通过将遍历p的指针前移来达到p后移的效果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
for(int i = 1, j = 0; i <= n; i++)
{
    while(j && s[i] != p[j + 1]) j = ne[j];
    //如果j有对应p串的元素， 且s[i] != p[j+1], 则失配， 移动p串
    //用while是由于移动后可能仍然失配，所以要继续移动直到匹配或整个p串移到后面（j = 0)

    if(s[i] == p[j + 1]) j++;
    //当前元素匹配，j移向p串下一位
    if(j == m)
    {
        //匹配成功，进行相关操作
        j = next[j];  //继续匹配下一个子串
    }
}

Trie 树

算法定义 用于快速存储和查找字符串集合的树。

实现思想

  • son[N][26] 存放小写字母，因此每个节点最多可以扩展出26边，每代表一个点，每列代表该节点扩展出一条边。
  • cnt[i] 以当前第i个结尾的有单词则为1，否则为0。
  • idx 下标，idx为0时，即代表根节点，又是空节点。

代码模板 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
//数组模拟的指针
#include<iostream>

using namespace std;
const int N = 100010;

char str[N];
int son[N][26], cnt[N], idx;
//son[N][26]: 存放小写字母，因此每个节点最多可以扩展出26条边
//cnt[N]: 以当前节点扩展的节点有多少个。
//idx: 下标，idx为0是既代表根节点，又是空节点

//插入函数
void insert(char str[]){
   	int p = 0;  // 每个单词都是从第一行开始，
    for(int i = 0; str[i]; i++) {
       	int u = str[i] - 'a'; // 将小写字母转换为0~25的数字
        if(!son[p][u]) son[p][u] = ++idx;  //如果p这个节点不存在u这个子节点
        p = son[p][u];  //跳转到p行
    }
    cnt[p] ++;  // 
} 
//查询函数
int query(char str[]){
    int p = 0;
    for(int i = 0; str[i]; i++) {
        int u = str[i] - 'a';
        if(!son[p][u]) return 0; //如果p后没有u节点，则直接输出0
        p = son[p][u];
    }
    return cnt[p];
}

并查集

目的： 在近乎O(1)的时间复杂度内支持下面两个操作

​ 1.将两个集合合并；

​ 2.询问两个元素是否在一个集合中；

原理：每个集合用一颗树表示，树根的编号就是整个集合的编号，每个节点存储它的父节点，p[x]表示x的父节点。若p[x] == x，则x为根节点

问题1： 如何判断树根节点： if(p[x] == x)

问题2： 如何求x的集合编号：while(p[x] != x) x = p[x] ；

问题3： 如何合并两个集合： p[x]是x的集合编号，p[y]是y的集合编号，则p[x] = y ；

优化：路径压缩： 当查询过一遍后，将路径上所有的节点直接指向根节点。

代码模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include<iostream>
using namespace std;

int p[N]; //存放每个节点的父节点，第i个节点的父节点为p[i]

// 返回x的祖宗节点 + 路径压缩（优化）
int find(int x){
    if(p[x] != x) // 如果不是根节点
        p[x] = find(x);
    return p[x];
}                                                                                                                                           
// 合并x，y所在的两个集合
int merge(int x, int y){
    p[find(x)] = find(y);  //将x的祖宗节点的父节点设置为 y的祖宗节点
}

// 判断x，y是否在同一集合中
bool Judge(int x, int y){
    if(find(x) == find(y))	//祖宗节点是同一个
        return true;
    return false;
}

堆

作用 维护一个数据集合；

需要实现的操作

  • 插入一个数；heap[++size] = x; up(size)
  • 求集合当中的最小值；heap[1];
  • 删除最小值；heap[1] = heap[size]; size—; down(1);
  • 删除任意元素；heap[k] = heap[size]; size—; down(k); up(k);
  • 修改任意元素；heap[k] = x; down(size); up(size);

基本结构 是一颗完全二叉树（除了最后一层节点之外，上层节点都是非空，最后一层节点是从左到右依次排布）

  • 小根堆：每个节点都满足小于等于左右两边的节点。

存储数据结构 使用数组存储，1号节点是根节点（下标从1开始），左儿子是2x ；右儿子是2x+1

  • h[N]存储堆中的值, h[1]是堆顶，x的左儿子是2x, 右儿子是2x + 1
  • ph[k]存储第k个插入的点在堆中的位置
  • hp[k]存储堆中下标是k的点是第几个插入的
  • size 堆中元素的个数

需要的操作

  • down(x) 将x节点往下移
  • up(x) 将x节点往上移
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
// h[N]存储堆中的值, h[1]是堆顶，x的左儿子是2x, 右儿子是2x + 1
// ph[k]存储第k个插入的点在堆中的位置
// hp[k]存储堆中下标是k的点是第几个插入的
int h[N], ph[N], hp[N], size;

// 交换两个点，及其映射关系
void heap_swap(int a, int b)
{
    swap(ph[hp[a]],ph[hp[b]]);
    swap(hp[a], hp[b]);
    swap(h[a], h[b]);
}

void down(int u)
{
    int t = u;
    if (u * 2 <= size && h[u * 2] < h[t]) t = u * 2;  // 存在左孩子并且左孩子比较小
    if (u * 2 + 1 <= size && h[u * 2 + 1] < h[t]) t = u * 2 + 1;  // 存在右孩子并且有孩子比较小
    if (u != t)
    {
        heap_swap(u, t); // 交换父亲节点 和 相对较小的子节点 
        down(t);  //递归遍历
    }
}

void up(int u)
{
    while (u / 2 && h[u] < h[u / 2])
    {
        heap_swap(u, u / 2);
        u >>= 1;
    }
}

// O(n)建堆
for (int i = n / 2; i; i -- ) down(i);

哈希表

  • 存储结构 ：下面两种方法是为了解决映射冲突的。映射冲突是指将两个不同的数映射到同一个数上。
    • 开放寻址法
    • 拉链法：形状类似于邻接表，将映射到同一个位置的数用一个链放在下面。
  • 字符串哈希方式

作用 ：将一堆较大范围的数映射到较小范围的一堆数中。

STL简介

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
vector, 变长数组，倍增的思想
    size()  返回元素个数
    empty()  返回是否为空
    clear()  清空
    front()/back()
    push_back()/pop_back()
    begin()/end()
    []
    支持比较运算，按字典序

pair<int, int>
    first, 第一个元素
    second, 第二个元素
    支持比较运算，以first为第一关键字，以second为第二关键字（字典序）

string，字符串
    size()/length()  返回字符串长度
    empty()
    clear()
    substr(起始下标，(子串长度))  返回子串
    c_str()  返回字符串所在字符数组的起始地址

queue, 队列
    size()
    empty()
    push()  向队尾插入一个元素
    front()  返回队头元素
    back()  返回队尾元素
    pop()  弹出队头元素

priority_queue, 优先队列，默认是大根堆
    size()
    empty()
    push()  插入一个元素
    top()  返回堆顶元素
    pop()  弹出堆顶元素
    定义成小根堆的方式：priority_queue<int, vector<int>, greater<int>> q;

stack, 栈
    size()
    empty()
    push()  向栈顶插入一个元素
    top()  返回栈顶元素
    pop()  弹出栈顶元素

deque, 双端队列
    size()
    empty()
    clear()
    front()/back()
    push_back()/pop_back()
    push_front()/pop_front()
    begin()/end()
    []

set, map, multiset, multimap, 基于平衡二叉树（红黑树），动态维护有序序列
    size()
    empty()
    clear()
    begin()/end()
    ++, -- 返回前驱和后继，时间复杂度 O(logn)

    set/multiset
        insert()  插入一个数
        find()  查找一个数
        count()  返回某一个数的个数
        erase()
            (1) 输入是一个数x，删除所有x   O(k + logn)
            (2) 输入一个迭代器，删除这个迭代器
        lower_bound()/upper_bound()
            lower_bound(x)  返回大于等于x的最小的数的迭代器
            upper_bound(x)  返回大于x的最小的数的迭代器
    map/multimap
        insert()  插入的数是一个pair
        erase()  输入的参数是pair或者迭代器
        find()
        []  注意multimap不支持此操作。 时间复杂度是 O(logn)
        lower_bound()/upper_bound()

unordered_set, unordered_map, unordered_multiset, unordered_multimap, 哈希表
    和上面类似，增删改查的时间复杂度是 O(1)
    不支持 lower_bound()/upper_bound()， 迭代器的++，--

bitset, 圧位
    bitset<10000> s;
    ~, &, |, ^
    >>, <<
    ==, !=
    []

    count()  返回有多少个1

    any()  判断是否至少有一个1
    none()  判断是否全为0

    set()  把所有位置成1
    set(k, v)  将第k位变成v
    reset()  把所有位变成0
    flip()  等价于~
    flip(k) 把第k位取反

搜索与图论

DFS与BFS

对比

数据结构 空间 性质
DFS stack O(h) 不具有最短性
BFS queue O(2^h^) “最短路”

深度优先搜索 DFS

算法： 回溯、剪枝

宽度优先搜索 BFS

类似于层序遍历

树与图的遍历：拓扑排序

树是一种特殊的图

树与图的存储

  • 有向图
    • 邻接矩阵：二维数组，适用于稠密图，T(n) = O(n ^ 2)
    • 邻接表：n个节点对应n个单链表，适用于稀疏图。

邻接表

  • h[N]：所有头节点的集合
  • e[N]：存每个节点的值
  • ne[N]：存每个节点的next值
1
2
3
4
5
6
7
8
9
10
11
12
// 对于每个点k，开一个单链表，存储k所有可以走到的点。h[k]存储这个单链表的头结点
int h[N], e[N], ne[N], idx;

// 添加一条边a->b
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ; // 头插
}

// 初始化
idx = 0;
memset(h, -1, sizeof h);

树与图的深度优先遍历

只考虑有向图即可。

  • 时间复杂度：O(n + m)，n表示点数，m表示边数

代码模板 

1
2
3
4
5
6
7
8
9
10
int dfs(int u)
{
    st[u] = true; // st[u] 表示点u已经被遍历过

    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j]) dfs(j);
    }
}

树与图的宽度优先遍历

  • 需要使用到队列，在对二叉树使用宽度有点遍历时，其实就是对二叉树进行层序遍历。

代码模板 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
queue<int> q;
st[1] = true; // 表示1号点已经被遍历过
q.push(1);

while (q.size())
{
    int t = q.front();
    q.pop();

    for (int i = h[t]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j])
        {
            st[j] = true; // 表示点j已经被遍历过
            q.push(j);
        }
    }
}

拓扑排序

  • 时间复杂度：O(n + m)，n表示点数，m表示边数

代码模板 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
bool topsort()
{
    int hh = 0, tt = -1;

    // d[i] 存储点i的入度
    for (int i = 1; i <= n; i ++ )
        if (!d[i])
            q[ ++ tt] = i;

    while (hh <= tt)
    {
        int t = q[hh ++ ];

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (-- d[j] == 0)
                q[ ++ tt] = j;
        }
    }

    // 如果所有点都入队了，说明存在拓扑序列；否则不存在拓扑序列。
    return tt == n - 1;
}

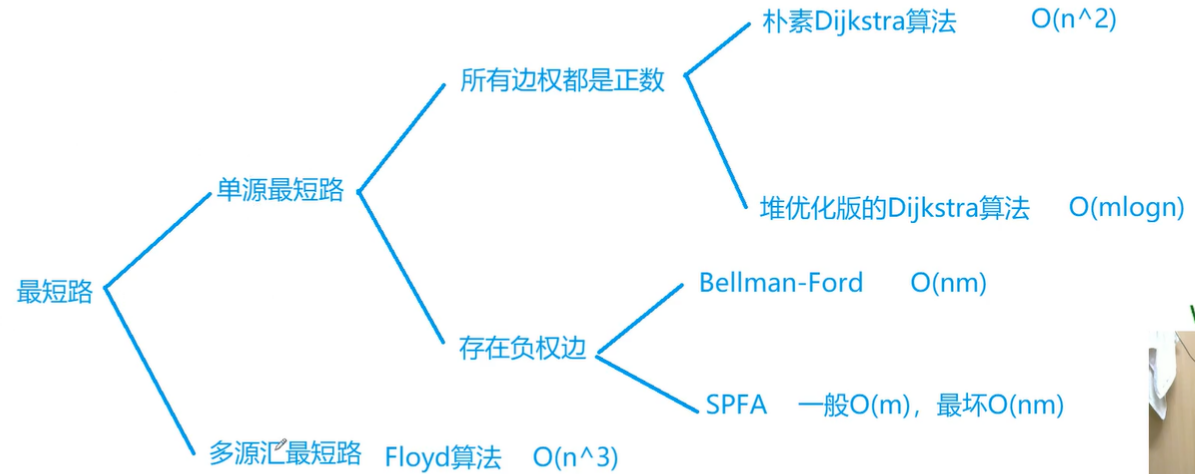
最短路径问题

常见的最短路径问题 ：n点的数量，m边的数量。

  • 单源最短路径
    • 所有边权都是正数
      • 朴素Dijkstra算法 ：O(n^2) 适用于稠密图
      • 堆优化版的Dijkstra算法：O(m * logn) 适用于稀疏图
    • 存在负权边
      • Bellman-Ford ： O(nm)
      • SPFA : 一般是O(m)，最坏是O(nm)
  • 多源汇最短路径 ：
    • Floyd算法：O(n^3)

shortLoad

朴素Dijkstra

  • 使用邻接矩阵存储，有向图：无向图是一种特殊的有向图。
  • s[i] ：当前已确定最短路径的点。
  • dist[i] ：第i个节点距离起点(1号点)的距离。初始化dist[1] = 0、disst[i] = +Max
  • g[N][N] ：存储每条边，下标从1开始

Dijkstra

代码模板 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
int g[N][N];  // 存储每条边
int dist[N];  // 存储1号点到每个点的最短距离
bool st[N];   // 存储每个点的最短路是否已经确定，false:未确定，true：已确定

// 求1号点到n号点的最短路，如果不存在则返回-1
int dijkstra()
{
    memset(dist, 0x3f, sizeof dist); // 初始化dist数组，将每个元素初始化为正无穷大。
    dist[1] = 0;

    for (int i = 0; i < n - 1; i ++ ) // 循环前n-1个节点即可，最后一个节点不用判断。
    {
        int t = -1;     // 在还未确定最短路的点中，寻找距离最小的点
        for (int j = 1; j <= n; j ++ )
            if (!st[j] && (t == -1 || dist[t] > dist[j])) //在所有st[j] == false 中找到dist最下的点。
                t = j;

        // 用t更新其他点的距离
        for (int j = 1; j <= n; j ++ )
            dist[j] = min(dist[j], dist[t] + g[t][j]);

        st[t] = true;
    }

    if (dist[n] == 0x3f3f3f3f) return -1;  // 第一个节点和n不连通
    return dist[n];
}

堆优化版的Dijkstra

  • 使用堆对朴素Dijkstra算法进行优化
  • 堆：使用c++里面的优先队列。
  • 数据结构：因为针对稀疏图，所以采用邻接表的方式存储。

代码模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
typedef pair<int, int> PII;

int n;      // 点的数量
int h[N], w[N], e[N], ne[N], idx;       // 邻接表存储所有边
int dist[N];        // 存储所有点到1号点的距离
bool st[N];     // 存储每个点的最短距离是否已确定

// 求1号点到n号点的最短距离，如果不存在，则返回-1
int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    priority_queue<PII, vector<PII>, greater<PII>> heap; // 定义优先队列代替堆，这样定义是小根堆
    heap.push({0, 1});      // first存储距离，second存储节点编号

    while (heap.size())
    {
        auto t = heap.top();
        heap.pop();

        int ver = t.second, distance = t.first;

        if (st[ver]) continue;
        st[ver] = true;

        for (int i = h[ver]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > distance + w[i])
            {
                dist[j] = distance + w[i];
                heap.push({dist[j], j});
            }
        }
    }

    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

数学知识

数论

质数

Def 在大于1的整数中，如果只包含1和整数这两个约数，就被称为质数，或者素数。

质数的判定—试除法

实现思想 ：i 从 2 枚举到 $\sqrt{n}$ 会缩减循环，但是sqrt(n)执行较慢，所以不使用。O(sqrt(n))

1
2
3
4
5
6
7
8
bool is_prime(int x)
{
    if (x < 2) return false;
    for (int i = 2; i <= x / i; i ++ )
        if (x % i == 0)
            return false;
    return true;
}

分解质因数—试除法

实现思想：从小到大枚举所有数，O(sqrt(n))。

1
2
3
4
5
6
7
8
9
10
11
12
void divide(int x)
{
    for (int i = 2; i <= x / i; i ++ )
        if (x % i == 0) // i 一定是质数
        {
            int s = 0;
            while (x % i == 0) x /= i, s ++ ;
            cout << i << ' ' << s << endl;
        }
    if (x > 1) cout << x << ' ' << 1 << endl;
    cout << endl;
}

朴素筛法求素数—埃氏筛法

实现思想：从2遍历到n，遍历到第i个数的时候，若该数没有被删除，则加入质数数组，然后删除该数的所有倍数。O(n * loglogn)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int primes[N], cnt;     // primes[]存储所有素数
bool st[N];         // st[x]存储x是否被筛掉

void get_primes(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (st[i]) continue; //如果第i个数已经被删掉，跳过
        primes[cnt ++ ] = i; // 如果第i个数还没有被删掉，则说明从2~i-1没有值是i的因子
        // 删除 质数i 的所有倍数，这里仅删除质数的倍数
        for (int j = i + i; j <= n; j += i)
            st[j] = true;
    }
}

线性筛法求素数

线性筛法求素数

相较于埃氏筛法快将近一倍。

实现思想：n只会被它的最小质因子筛掉。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int primes[N], cnt;     // primes[]存储所有素数
bool st[N];         // st[x]存储x是否被筛掉

void get_primes(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i; // 如果是质数，加入至质数数组
        // 从小到大枚举所有的质数
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break; // primes[j] 一定是i的最小质因子
        }
    }
}

约数

试除法求所有约数

实现思想类似于试除法求质数。O(sqrt(n)) 

1
2
3
4
5
6
7
8
9
10
11
12
vector<int> get_divisors(int x)  //使用vector数组存放所有约数
{
    vector<int> res;
    for (int i = 1; i <= x / i; i ++ )
        if (x % i == 0)
        {
            res.push_back(i);
            if (i != x / i) res.push_back(x / i);
        }
    sort(res.begin(), res.end());
    return res;
}

约数个数

1
2
3
如果 N = p1^c1 * p2^c2 * ... *pk^ck
约数个数： (c1 + 1) * (c2 + 1) * ... * (ck + 1)
约数之和： (p1^0 + p1^1 + ... + p1^c1) * ... * (pk^0 + pk^1 + ... + pk^ck)

组合计数

高斯消元

简单博弈论

正在加载今日诗词....